Regression 回归例子
学习资料:
导入模块 ¶
在上一节课程中,我么学习了如何利用Theano定义神经网络的层类,我们设计了一个Layer类来规划神经网络层的信息。
这节我们学习如何利用神经网络解决简单的回归问题。 首先,和之前所有的练习一样,我们引入需要使用的Python包:
import theano
import theano.tensor as T
import numpy as np
import matplotlib.pyplot as plt
与之前的代码不同的地方是我们在这里引入了matplotlib这个工具包, 用来实现绘图及数据可视化。
大家可以利用我的视频教程来学习或复习 Matplotlib 这个工具: Matplotlib 数据可视化神器 Python。
定义层结构 ¶
接下来我们声明我们的Layer类。 对于神经网络的每个Layer,
它需要具备输入来源input,输入神经元维度in_size,输出神经元纬度out_size,
和我们之前设计的神经元的激活函数activation_function, 默认为None。
这段代码和上节课一致,此处不再重复。
class Layer(object):
def __init__(self, inputs, in_size, out_size, activation_function=None):
self.W = theano.shared(np.random.normal(0, 1, (in_size, out_size)))
self.b = theano.shared(np.zeros((out_size, )) + 0.1)
self.Wx_plus_b = T.dot(inputs, self.W) + self.b
self.activation_function = activation_function
if activation_function is None:
self.outputs = self.Wx_plus_b
else:
self.outputs = self.activation_function(self.Wx_plus_b)
伪造数据 ¶
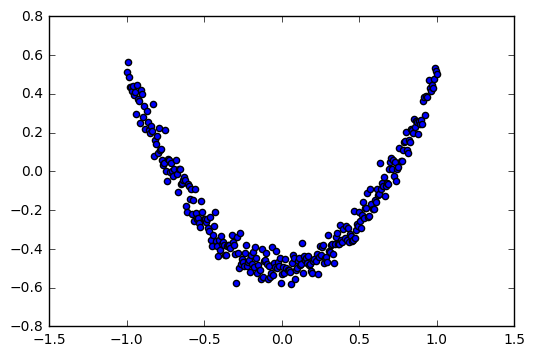
接下来,我们首先人工生成一个简单的带有白噪声的一维数据 y = x^2 - 0.5 + noise。
# Make up some fake data
x_data = np.linspace(-1, 1, 300)[:, np.newaxis]
noise = np.random.normal(0, 0.05, x_data.shape)
y_data = np.square(x_data) - 0.5 + noise # y = x^2 - 0.5 + wihtenoise
然后,我们用散点图(Scatter)把它显示出来, 横轴是x_data, 纵轴是y_data。
# show the fake data
plt.scatter(x_data, y_data)
plt.show()
显示结果:
搭建网络 ¶
然后,我们定义神经网络的输入与目标;
# determine the inputs dtype
x = T.dmatrix("x")
y = T.dmatrix("y")
这里,T.dmatrix 意味着我使用的是float64的数据类型, 和我的输入数据一致。
接着我们设计我们的神经网络,它包括两层,构成1-10-1的结构。
对于l1我们的input_size要和我们的x_data一致,然后我们假设了该层有10个神经元,并且以relu作为激活函数。
所以,l2以l1.output为输入,同时呢,它的输出为1维,和我们的y_data保持一致,作为神经网络的输出层,我们采用默认的线性激活函数。
# determine the inputs dtype
# add layers
l1 = Layer(x, 1, 10, T.nnet.relu)
l2 = Layer(l1.outputs, 10, 1, None)
然后,我们定义一个cost,也就是损失函数(cost/loss function),我们采用的是l2.outputs 神经网络输出与目标值y的的平均平方差。
# compute the cost
cost = T.mean(T.square(l2.outputs - y))
根据 cost 我们可以计算我们神经网络权值和偏置值的梯度(gradient), 这里Theano已经集成好了对应的函数:
# compute the gradients
gW1, gb1, gW2, gb2 = T.grad(cost, [l1.W, l1.b, l2.W, l2.b])
有了以上的基本运算步骤后,我们就可以开始,利用梯度下降法训练我们的神经网络。
首先我们定义一个学习率 learning_rate, 这个学习率的取值一般是根据数据及实验的经验估计的,它会对模型的收敛性造成一定的影响,一般倾向于采用较小的数值。
然后,我们定义train这个函数来描述我们的训练过程,首先我们定义了函数的输入inputs=[x, y], 函数的输出为outputs=cost, 同时更新网络的参数。
# apply gradient descent
learning_rate = 0.05
train = theano.function(
inputs=[x, y],
outputs=cost,
updates=[(l1.W, l1.W - learning_rate * gW1),
(l1.b, l1.b - learning_rate * gb1),
(l2.W, l2.W - learning_rate * gW2),
(l2.b, l2.b - learning_rate * gb2)])
然后我们定义一个预测函数来输出我们最终的结果predict.
# prediction
predict = theano.function(inputs=[x], outputs=l2.outputs)
训练 ¶
最后,我们就要开始真正的训练啦!我们要把神经网络训练1000次,同时呢每训练50次时就输出此时的误差(cost):
for i in range(1000):
# training
err = train(x_data, y_data)
if i % 50 == 0:
print(err)
你大概会得到一下类似的结果:
"""
2.2858426513500967
0.011148671551881364
0.008641346716060181
0.007188403510180637
0.006250296000631469
0.005628021126864056
0.005142288453451058
0.004793442944984919
0.004539827398288326
0.004376693858775578
0.0042555015795511615
0.004156078781653181
0.0040801312408181726
0.004022424092526545
0.003974514689028584
0.003934815285052449
0.0039030377541023824
0.003875222239897254
0.003848930488582809
0.0038275646534826836
"""
结果显示我们的训练误差是在不断的减小的,也就是说我们的神经网络在一点一点的逼近目标值。
再下一小节中我们将学习使用matplotlib来动态的显示我们训练的神经网络的预测结果。
分享到:
![]()
![]()
![]()
![]()
如果你觉得这篇文章或视频对你的学习很有帮助, 请你也分享它, 让它能再次帮助到更多的需要学习的人.
莫烦没有正式的经济来源, 如果你也想支持 莫烦Python 并看到更好的教学内容, 赞助他一点点, 作为鼓励他继续开源的动力.